研究要旨

　格子点に関する問題を解く中で,有理数にまつわる図形問題に興味を抱くようになり,単位正方形の内部に,すべての頂点からの距離が有理数となる点が存在するのか?という命題について調べたところ,未解決問題であることがわかったため,研究に着手した。

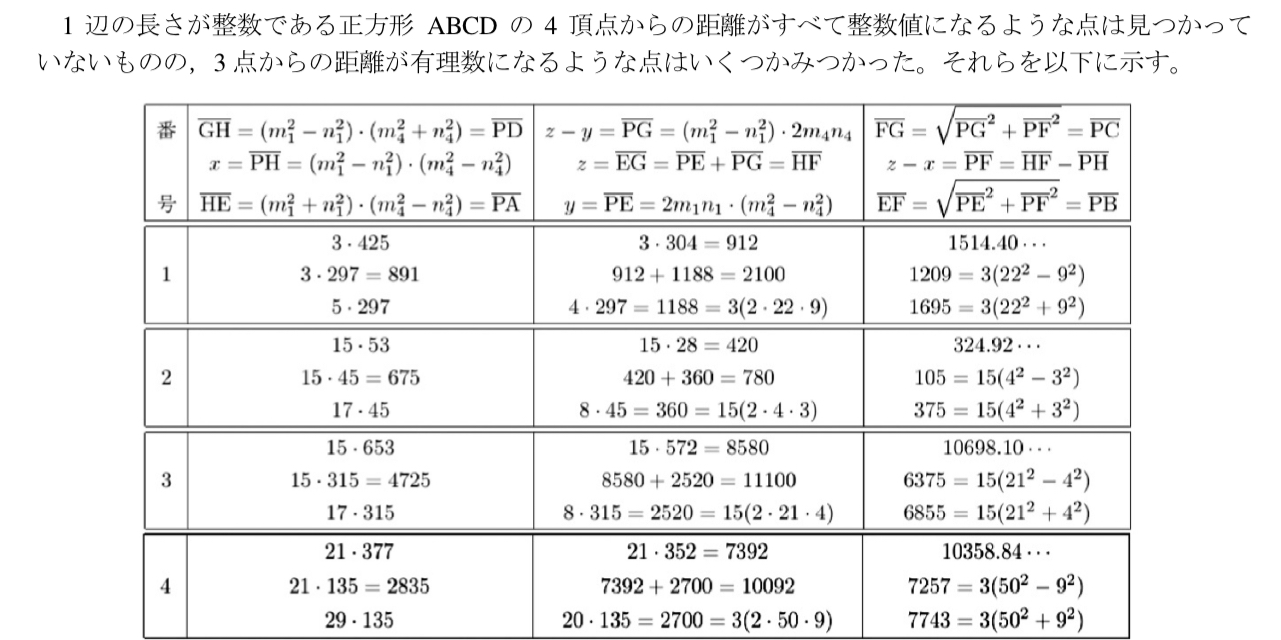
　本研究では全有理距離点問題を同値変形して整数問題に帰着させ,全有理距離点が存在する場合に満たすべき条件について考察する。なお,Guy(1994)は,単位正方形の3頂点からの距離が有理数となるような点は (s²+b²−a²)²+(s²+b²−c²)²=(2bs)² … (1) の整数解から得られることを示したほか,John Conway と Mike Guy によって,この方程式に無限個の整数解があると示唆されたことを記述している。さらに,4つ目の頂点との距離も整数値(縮小すれば有理数値)になるためには, a²+c²=b²+d²… (2) が成り立つことが必要である。また,Berry (1990)によって,(1) (2)に対応する2式について2次式,4次式,6次式,8次式で与えられるような (1)の解が与えられ,2次,4次のものについては,(2) を満たすものはないことが証明された。

著者

吉岡 拓人

Title

The problem of a point at a rational distance from each corner of a unit square

Abstract

I studied whether there exists a point in the unit square where all distances from each vertex are rational numbers (hereinafter referred to as an all-distance rational point). I placed the unit square in a coordinate plane and considered the assumption that an all-distance rational point exists, and found that this point represents a rational point and can exist only on lines that can be represented in a certain form.

Author

Yoshioka T.